CIS194 4강 고차 프로그래밍과 타입 추론에 있는 연습문제 풀이입니다.
통밀 프로그래밍
fun1
fun1이 하는 일을 파악해 보자.
- 빈 리스트의 경우 1을 반환
- 리스트에 원소가 있는 경우
- 헤드 원소가 짝수인 경우
- 헤드 원소에서 2를 뺌
- 나머지 원소들에 대해서는 다시
fun1을 적용 - 위 두 값을 곱해서 결과로 함
- 헤드 원소가 홀수인 경우
- 그냥 나머지 원소에 대해
fun1을 적용
- 그냥 나머지 원소에 대해
- 헤드 원소가 짝수인 경우
따라서 실제로 이 함수는 리스트에 있는 모든 짝수인 원소들에 대해서 2를 뺀 수를 모두 곱하는 함수다. 여기까지 파악됐으면 아주 쉽게 다음과 같이 해를 구현할 수 있다. -연산의 부분적용시 \x -> x - 2를 (- 2)로 간략히 표기할 수 있어야 하지만(이를 섹션(section)이라고 한다), 음수 단항 연산자 -와 구분할 수 없기 때문에 어쩔 수 없이 subtract라는 함수를 사용해야 한다. 한가지 유의할 점은 subtract는 (-)와 피연산자 순서가 반대라는 점이다. 하지만 피연산자 순서가 반대라는 사실로 인해 (subtract 2)라고 하면 우리가 애초 의도했던 (- 2)와 정확히 같은 역할을 한다. 참고로 (+ 2)는 섹션이지만 (subtract 2)는 그냥 함수 부분적용이다.
부분적용
(-) 2와 섹션(- 2)를 혼동하지 말라!혹시
-연산자를 괄호로 감싸서 함수 표현을 쓰고 이를 섹션처럼()안에 묶으면 되지 않을까 생각하는 독자도 있을 것이다. 하지만((-) 2)는 그냥 괄호가 없는(-) 2와 같고, 이는-의 첫번째 피 연산자를 2로 부분적용한 함수에 지나지 않는다. 섹션도 부분적용이고(-) 2도 부분적용이라서 우연히도 두 함수의 타입은 같기 때문에 컴파일시 아무 문제가 없지만 결과 값은 달라진다는 점에 유의하라.
fun1' :: [Integer] -> Integer
fun1' = product . (map (subtract 2)) . (filter even)
아니면 필터와 폴드 연산을 사용할 수도 있을 것이다. 곱셈은 순서와 관계 없으므로 foldr이나 foldl 모두 문제가 없다. foldl과 foldr의 타입을 살펴보면서 리스트의 원소 타입(a)과 폴드 결과 생기는 전체 요약 값의 타입(b)에 맞춰 종합해주는 연산의 피연산자를 제대로 사용해 주기만 하면 된다. foldl을 사용하면 b -> a -> b 타입이므로 첫번째 인자가 결과값(각 원소에 -2를 한 다음 곱한 값)이고 두번째 인자가 현재 원소 값이다.
fun1'' :: [Integer] -> Integer
fun1'' = (foldl (\p x -> (x-2) * p) 1) . (filter even)
포인트프리 표현
재미삼아 여기서 \p x -> (x-2) * p를 포인트프리로 표현한 식이 어떻게 되는지 찾아보자. pointfree.io에서 변환해 본 결과는 다음과 같다.
(. subtract 2) . (*)
해석해 볼 수 있을까? 한번 고민해보기 바란다. 다음은 각 함수의 정의를 따라 다시 역으로 포인트를 다 보여가면서 펼쳐보이는 과정이다.
(. subtract 2) . (*)
=== \x -> (. subtract 2) ((*) x) -- 중위 . 없앰
=== \x -> (. subtract 2) ((\a b -> a * b) x) -- (*)를 펼침
=== \x -> (. subtract 2) (\b -> x * b) -- 함수 적용
=== \x -> (\f -> f . (subtract 2)) (\y -> x * y) -- (. subtract 2) 섹션을 풀어씀
=== \x -> (\y -> x * y) . (subtract 2) -- 함수 적용
=== \x -> { \xx -> (\y -> x * y) (( subtract 2 ) xx ) } -- 중위 . 없앰
=== \x -> { \xx -> (\y -> x * y) (xx - 2)} -- subtract 적용
=== \x -> { \xx -> x * (xx - 2) } -- \y -> ... 람다에 (xx - 2) 적용
=== \x -> \xx -> x * (xx - 2) -- -> 우선순위에 따라 괄호 없앰
=== \x -> \y -> x * (y - 2) -- 변수 이름만 바꿈(alpha conversion)
=== \x y -> x * (y - 2) -- 인자 여럿인 람다 줄여쓰기
=== \x y -> (y-2) * x -- * 교환법칙
<=> \p x -> (x-2) * p
원래의 함수 \p x -> (x-2) * p와 비교해보면 같다!
fun2
iterate와 takeWhile이라는 힌트를 두고 생각해 보면, Integer -> Integer 재귀 함수를 직접 푸는 것이 아니라 Integer의 시퀀스를 만들고 그 중에 우리가 원하는 성질의 값을 택하라는 이야기 같다.
프렐류드에서 iterate를 보면 다음과 같은 설명을 볼 수 있다.
`iterate f x`는 `x`에 `f`를 반복적용한 결과를 무한 리스트로 반환한다.
iterate f x == [x, f x, f (f x), ...]
일단 우리가 관심 있는 값은 fun2에 인자로 넘어가는 값 들이다. 다음과 같이 그런 시퀀스를 만들 수 있을 것이다.
iterate (\n -> if (even n) then (n `div` 2) else (3 * n + 1))
이제 이 시퀀스를 1이 아닌 동안만 취하면 우리가 원하는 시퀀스를 얻을 수 있다.
takeWhile (/= 1) (iterate (\n -> if (even n) then (n `div` 2) else (3 * n + 1)))
예를 들어 10을 가지고 해보면 10,5,16,8,4,2라는 결과를 얻을 수 있다.
실제 fun2가 더하는 숫자들은 자신이 입력으로 받은 값 중에 짝수들 뿐이다. 따라서 최종 결과는 이 시퀀스에서 짝수만을 filter해서 sum 하면 된다.
fun2' :: Integer -> Integer
fun2' = sum . (filter even) . (takeWhile (/= 1)) . (iterate (\n -> if (even n) then (n `div` 2) else (3 * n + 1)))
함수 합성 .과 부분적용(또는 섹션)에 익숙해지도록 하라. 이렇게 간단한 경우 쉽게쉽게 포인트프리 폼을 사용할 수 있으면 코딩이 쾌적해진다. 간단하게 .를 쓸 때 . 연산자의 오른쪽 피연산자 함수의 결과 타입이 왼쪽 피연산자 함수의 입력 타입과 일치해야 한다는 점을 염두에 두고 코드를 작성한다면 좀 더 쉽게 어떤 함수를 만들어야 할지 알 수 있다.
여기서도 filter even까지 부분 적용하면 리스트에서 짝수만을 걸러내서 리스트를 반환하는 함수가 생기고, iterate \n ...을 부분적용하면 정수를 받아서 리스트를 반환하는 함수가 생기고, takeWhile (/= 1)을 부분적용하면 리스트 맨 앞부터 1이 아닌 원소가 최초로 나타나기 직전까지의 원소들로 이뤄진 리스트를 얻을 수 있다는 점을 부분적용에 익숙해지고 나면 쉽게 생각할 수 있다.
트리 폴딩
foldTree의 타입과 foldr의 타입을 일단 살펴보자.
foldTree :: [a] -> Tree a
foldr :: Foldable t => (a -> b -> b) -> b -> t a -> b
여기서 t a는 그냥 폴드를 적용 가능한 타입인데 원소 타입이 a라는 뜻으로 생각하면 된다. 리스트도 Foldable하기 때문에 t a를 [a]로 생각하면 된다. 만들어낼 최종 타입은 Tree a였다. 따라서 b를 Tree a로 대치해야 한다. 따라서 실제 우리가 foldr을 사용할 때의 타입은 다음과 같다고 생각할 수 있다.
foldr :: (a -> Tree a -> Tree a) -> Tree a -> [a] -> Tree a
foldr의 두번째 인자인 초깃값은 자연스럽게 Leaf가 될 것이다. [a]는 foldTree가 입력으로 받은 리스트가 될 것이다. 남은 것은 첫번째 인자인 함수 a -> Tree a -> Tree a를 어떻게 정의할 것인가이다.
여기서는 트리가 균형트리여야 한다는 제약만 존재하므로 a 타입의 입력값 자체는 트리 구축에 그리 중요하지 않고, 기존 트리의 형태만이 중요하다. 매 단계마다 새 원소와 현재까지 구축한 트리를 가지고 새 트리를 구축해야 한다. 이때 균형을 유지해야 한다. 입력받은 기존 트리의 모양에 따라 해야할 일을 분류해보자.
- 기존 트리가
Leaf인 경우:a타입의 값을 트리에 넣어야 한다. 따라서Node를 하나 만들면서 좌우변을 모두Leaf로 하고a타입의 값을(x라고 부르자) 루트에 넣는다. 이때 트리 높이는 0이 될 것이다. 결과적으로Node 0 Leaf x Leaf가 생긴다. - 기존 트리의 높이가 0인 경우: 기존 트리가 루트밖에 없는 트리이므로 새로 노드를 만들면서 왼쪽 서브트리에 기존 트리를 넣자. 결과적으로
Node 1 (기존트리) x Leaf가 된다. - 기존 트리의 높이가 1 이상인 경우: 좌변과 우변의 높이를 비교해서 더 낮은 쪽에 원소
x를 삽입한다(이때 삽입은 이 함수를 재귀적으로 호출하면 된다). 좌우변 높이가 같은 경우 어느 한쪽을 선택해x를 삽입하면 된다. 편의상 왼쪽에 원소를 삽입하자.
여기서 트리의 높이를 알아내는 함수가 필요하다. 패턴매칭을 사용하면 쉽게 다음과 같이 정의할 수 있다.
height :: Tree a -> Integer
height Leaf = -1 -- 높이가 0인 트리도 있으므로 -1을 Leaf 노드의 높이로 잡자
height (Node h _ _ _) = h
앞의 알고리즘을 하스켈로 기술하면 다음과 같다.
insert :: a -> Tree a -> Tree a
insert x Leaf = Node 0 Leaf x Leaf
insert x (Node 0 Leaf v Leaf) = Node 1 (insert x Leaf) v Leaf
insert x (Node h left v right) =
let
leftH = height left
rightH = height right
in
if leftH > rightH then
Node h left v (insert x right)
else if leftH < rightH then
Node h (insert x left) v right
else
Node (h+1) (insert x left) v right
이제 foldr로 트리 구축 알고리즘을 만들 수 있다.
foldTree :: [a] -> Tree a
foldTree = foldr insert Leaf
폴드 연습하기
xor
foldr 등을 사용하면서 어떤 함수를 선택한다고 할 때 그 함수를 그냥 다음과 같이 if문 등으로 간단하게 정의할 수도 있다. true시에는 예전 상태를 그대로 반환하고, false시에는 이전 상태를 토글하면 되므로 다음과 같이 정의할 수 있다. False가 하나도 없거나 개수가 짝수면 False이므로 초기 값은 False가 들어가면 된다.
xor :: [Bool] -> Bool
xor = foldr (\x y -> if x then y else not y) False
다른 방법은 진리표를 사용해 로직식으로 표현하는 것이다.
| 원소 | 누적값 | 결과값 |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | T |
이는 ((not x) && (not y)) || (x && y)에 해당한다.
xor' :: [Bool] -> Bool
xor' = foldr (\x y -> ((not x) && (not y)) || (x && y)) False
map
참고로 foldr을 가지고 리스트를 쉽게 복사할 수 있다.
copy = foldr (:) []
람다를 사용해 직접 어떤 일을 하는지 구체적으로 표현하면 다음과 같다.
copy' = foldr (\x xs -> x : xs) []
이는 기본적으로 foldr의 함수 적용 순서가 리스트의 : 적용 순서와 같기 때문이다. 그림으로 표현하면 다음과 같다.
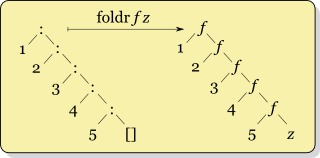
이를 활용하면 쉽게 map을 구현할 수 있다. :를 적용하기 전에 원소에 map의 인자로 전달받은 함수를 적용해 주면 된다.
map' :: (a -> b) -> [a] -> [b]
map' f = foldr (\x xs -> (f x) : xs) []
:와 f를 함성한 함수를 사용하는 방법
여기서 \x xs -> (f x) : xs를 다시 살펴보자. 함수 적용 순서를 찬찬히 생각해 보면, 이 함수는 x에 f를 적용한 결과에 :를 적용한 것과 같다. 연산자를 함수 형태로 표현하면
더 쉽게 이를 이해할 수 있다.
\x xs -> (:) (f x) xs
어떤 함수를 먼저 적용한 결과를 받아서 다른 함수에 적용한다는 말을 보면 함수 합성이 생각나야 한다. 따라서 위 람다 식은 다음과 같다.
(:) . f
이제 map을 다음과 같이 구현할 수 있다.
map'' :: (a -> b) -> [a] -> [b]
map'' f = foldr ((:).f) []
foldl을 foldr로 구현하기
foldl과 foldr의 결과는 다음과 같다.
foldr f zr [x1, x2, ..., xn] == x1 ‘f‘ (x2 ‘f‘ ... (xn ‘f‘ zr)...)
foldl g zl [x1, x2, ..., xn] == (...((zl ‘g‘ x1) ‘g‘ x2) ‘g‘...) ‘g‘ xn
만약 그냥 단순히 foldl g z1 = foldr f zr이 될 수 있는 g,f,zl,zr이 있다면 좋을 것이다.
그런 경우가 가능한지 가장 간단한 원소가 1개 밖에 없는 리스트를 바탕으로 생각해 보자.
foldr f zr [x1] == x1 ‘f‘ zr
foldl g zl [x1] == zl ‘g‘ x1
이 둘이 같으려면 f의 인자를 뒤집은 함수가 g가 되면 될것 같다. 즉, g x y = f y x이고, zr과 zl이 같으면 가장 단순한 경우다.
그렇다면 다음과 같이 쓸 수 있을 것이다.
foldl' g zl = foldr (\a b -> g b a) zl
괜찮을까? 하지만 심각한 문제가 있다. 이 정의를 원소가 2개인 리스트에 적용한 경우를 생각해 보자.
foldl f z = ((z `f` x1) `f` x2)
foldl' f z = foldr (\a b -> f b a) z
-------------- -> 이 부분을 편의상 g라고 하자.
= x1 `g` (x2 ‘g‘ z)
= x1 `g` (z `f` x2)
= (z `f` x2) `f` x1
함수 적용 순서가 거꾸로이다! 따라서 단순히 함수 적용 순서를 뒤집어주는 것 만으로는 foldl을 foldr로 정의할 수 없다. foldl에서 원소 적용 순서는 foldr 원소 적용 순서와 반대이다. 적용 순서가 반대라는 점을 생각해보면 함수 호출과 리턴의 관계가 생각난다. 호출 스택에서 함수 호출은 함수 반환과 역순이다. 이를 활용한다면 뭔가 좋은 방법이 있을 것 같다. 다시 원소 1개짜리 리스트를 생각해보자.
foldr f zr [x1] == x1 ‘f‘ zr
foldl g zl [x1] == zl ‘g‘ x1
여기서 x1 f zr이 어떤 함수를 만들어내고, 그 함수에 z1을 적용하면 zl g x1과 같은 결과를 만들어낸다고 생각하면 어떨까? 1개짜리 리스트를 가지고 생각해보면 다음과 같은 방식으로 쓸 수 있어야 한다고 생각할 수 있다.
foldl :: (b -> a -> b) -> b -> [a] -> b
foldl g zl [x1] = (foldr f zr [x1])(zl)
이 식에서 f의 타입은 뭘까? 일단 f의 첫번째 인자는 리스트의 원소 타입이므로 foldl의 리스트 원소 타입인 a이다. f의 두번째 인자는 zr이라는 어떤 값이다. 타입을 모르니 t라고 가정하자. f가 반환하는 함수는 zl을 받아서 원래 foldl의 결과와 같은 값을 내놓는 함수여야 한다. 타입만 따지면 따라서 이 함수는 b -> b가 된다. 즉, f의 타입은 a -> t -> (b -> b)이다(맨 마지막 괄호는 생략 가능). 그런데, foldr의 특성상 f의 두번째 인자와 반환값은 타입이 같아야 한다. 따라서 t는 b -> b라고 결론을 내릴 수 있다. 따라서 f의 타입은 a -> (b -> b) -> (b -> b)이다(맨 마지막 괄호는 생략 가능).
한편 foldr과 foldl의 결과와 바로 위에서 정의한 foldl 정의로부터 다음 등식을 얻을 수 있다.
zl `g` x1 = (x1 `f` zr)(zl) -- (1)
거꾸로 f의 입장에서 정리를 해보면 다음과 같을 것이다.
(f x1 zr)(zl) = g zl x1
f x1 zr이 만들어내는 함수는 zl을 받아서 g zl x1을 만들어내야 한다. zr을 무시하고 타입을 맞출 수도 있지만 그렇게 정의하면 원소가 2개 이상일 때 정보가 소실될 수 있다. zr을 무시하지 않는다면 zr이 b -> b 타입의 함수이고, g가 b -> a -> b 타입의 함수임을 감안하면 택할 수 있는 가지수는 몇가지 없다. g를 적용하기 전에 b 타입의 값에 zr을 적용하거나, g로 b 타입의 값을 만들어낸 다음에 zr을 적용해야 한다.
- 인자로 받은 값에
zr을 적용한 후g를 적용하는 경우:f x1 zr = \x -> g (zr x) x1 g먼저 적용한 후zr을 적용하는 경우:f x1 zr = \x -> zr (g x x1)
각각의 경우를 람다로 바꾸면 다음과 같다.
- 인자로 받은 값에
zr을 적용한 후g를 적용하는 경우:f = \x h y -> g (h y) x g먼저 적용한 후zr을 적용하는 경우:f = \x h y -> h (g y x)
fodlr의 정의에 의해 리스트가 2개라면 f x1 (f x2 zr)이 나온다. 이 식에 위 두 f를 넣어보면 다음과 같은 결과를 얻을 수 있다.
첫번째 f의 경우:
f x1 (f x2 zr) = f x1 {(\x h y -> g (h y) x) x2 zr}
= f x1 (\y -> g (zr y) x2)
= (\x' h' y' -> g (h' y') x') x1 (\y -> g (zr y) x2)
= \y' -> g ((\y -> g (zr y) x2) y') x1
= \y' -> g (g (zr y') x2) x1
따라서 {f x1 (f x2 zr)}(zl) = g (g (zr zl) x2) x1이 된다. zr이 어떤 함수든 이 결과의 문제는 g가 x1에 적용되기 전에 x2에 적용된다는 점이다.
두번째 f의 경우
f x1 (f x2 zr) = f x1 {(\x h y -> h (g y x)) x2 zr}
= f x1 (\y -> zr (g y x2))
= (\x' h' y' -> h' (g y' x')) x1 (\y -> zr (g y x2))
= \y' -> (\y -> zr (g y x2))(g y' x1)
= \y' -> zr (g (g y' x1) x2)
이경우 {f x1 (f x2 zr)}(zl) = zr (g (g zl x1) x2)가 된다. 이는 foldl의 결과와 같은 형태다. 한편 zr은 자연스럽게 id 즉, \x -> x 함수가 된다.
이를 정리하면 다음과 같다.
foldl' g zl xs = (foldr (\x h y -> h (g y x)) id xs)(zl)
이런식으로 타입을 따져가면서 구현해 보는 방식을 살펴보면 강력한 타입 시스템이 가능한 구현의 수를 줄여주는 측면이 있다는 사실을 알 수 있다.
순다람의 체
이론
일다 순다람의 체를 이해하도록 하자. 순다름의 체는 1부터 n까지의 정수 리스트로부터 1<=i<=j이면서 i + j + 2ij <= n인 모든 i + j + 2ij를 제거하고 남은 모든 수에 대해 2를 곱하고 1을 더해서 2n + 2 이하의 모든 소수를 구하는 방식이다.
예를 들어 n=4이라면, (i,j) 순서쌍은 (1,1)부터 (4,4)까지 16가지가 존재하며, 그중에 i가 j보다 큰 순서쌍을 제외하면 개수가 10가지로 줄어든다. 한편 그런 순서쌍 i+j가 3이상인 경우는 확실히 i+j+2ij도 4보다 커지므로 i+j는 2 이하여야 하고, i,j가 모두 1 이상이므로 결국 따져봐야 할 순서쌍은 (1,1)밖에 없다. 1+1+2 = 4 이므로 4를 제외하면 리스트에는 1,2,3만 남고, 이 수들을 2배해서 1 더하면 3, 5, 7이라는 세가지 소수가 남는다. 이 세 소수는 n=4일 때 10(2*4+2)이하의 모든 소수이다.
해법
일단 제외해야 하는 수의 목록을 구해보자. 다음과 같이 구하면 된다.
- 1부터 n까지 모든 순서쌍 (i,j)를 찾는다.
- 1의 결과 순서쌍 중에 i<=j인 순서쌍만 남긴다.
- 2의 결과 순서쌍 (i,j)를 i+j+2ij로 변환한다.
- 3의 결과 순서쌍 중에 n 이하인 수만 남긴다
이를 하스켈 코드로 옮기는 것은 아주 쉽다.
cartProd :: [a] -> [b] -> [(a, b)]
cartProd xs ys = [(x,y) | x <- xs, y <- ys]
sundExcl :: Integer -> [Integer]
sundExcl n = ((filter (\x->x<n)) . (map (\(i,j)->i+j+2*i*j)) . (filter (\(i,j)->i<=j)) . (\x->cartProd x x)) [1..n]
이렇게 구한 리스트는 제외해야 할 리스트이다. 따라서 [1..n]까지의 리스트에서 이렇게 구한 리스트를 제외해야 한다. 리스트를 정렬해서 빼는 알고리즘을 만들면 되겠지만 Data.Set을 사용해보자. fromList는 리스트에서 집합을 만들어주고, difference는 두 집합의 차이를 계산한다. 리스트를 다시 만들려면 toList를 쓰면 된다.
sieveSundaram :: Integer -> [Integer]
sieveSundaram n =
map (\n->2*n+1) (Data.Set.toList
(Data.Set.difference
(Data.Set.fromList [1..n])
(Data.Set.fromList (sundExcl n))))
하나로 합치기
한편 Data.Set을 임포트하고 나면 filter나 map을 사용할 때 ambiguous 하다는 오류가 나온다. 이를 방지하기 위해서는 import qualified를 사용해 Data.Set에서 임포트한 함수 앞에 꼭 한정사를 붙이게 만들어야 한다. 이를 활용해 순다람 체 전체 코드를 정리하면 다음과 같다.
import qualified Data.Set as Set
cartProd :: [a] -> [b] -> [(a, b)]
cartProd xs ys = [(x,y) | x <- xs, y <- ys]
sundExcl :: Integer -> [Integer]
sundExcl n = ((filter (\x->x<n)) . (map (\(i,j)->i+j+2*i*j)) . (filter (\(i,j)->i<=j)) . (\x->cartProd x x)) [1..n]
sieveSundaram :: Integer -> [Integer]
sieveSundaram n =
map (\n->2*n+1) (Set.toList
(Set.difference
(Set.fromList [1..n])
(Set.fromList (sundExcl n))))