이 글은 CIS 4강을 다룬 글입니다.

고차 프로그래밍과 타입 추론

무명 함수

100보다 큰 모든 Integer를 골라내는 graterThan100이라는 함수를 작성한다고 가정하자. 이 함수의 타입과 함수가 할 수 있는 일은 다음과 같다.

-- 타입
greaterThan100 :: [Integer] -> [Integer]

-- 할 수 있는 일
greaterThan100 [1,9,349,6,907,98,105] = [349,907,105]

지금까지 배운 내용을 가지고는 다음과 같이 이 함수를 작성할 수 있다.

gt100 :: Integer -> Bool
gt100 x = x > 100

greaterThan100 :: [Integer] -> [Integer]
greaterThan100 xs = filter gt100 xs

하지만 100보다 큰 수를 선택하는 술어 함수에 gt100이라는 이름을 부여하는 일을 귀찮다. 나중에 다시 쓸 일이 없는 일회성 함수에 일일히 이름을 붙여야 한다면 짜증날 것이다. 이럴 때 람다 추상화를 사용할 수 있다.

greaterThan100_2 :: [Integer] -> [Integer]
greaterThan100_2 xs = filter (\x -> x > 100) xs

\x -> x > 100에서 \는 그리스 문자 람다(λ)를 표현한다(짧은 다리를 생략한 것이다). 이 람다 식은 x를 인자로 받아서 x > 100 여부를 결과로 반환하는 함수다.

람다가 인자를 여럿 받을 수도 있다.

Prelude> (\x y z -> [x,2*y,3*z]) 5 6 3
[5,12,9]

한편, greaterThan100과 같은 특수한 경우에는 람다를 사용하지 않고 좀 더 간단하게 함수를 정의할 방법이 있다.

greaterThan100_3 :: [Integer] -> [Integer]
greaterThan100_3 xs = filter (>100) xs

여기서 >100은 연산자 섹션(operator section)이라고 부른다. 어떤 연산자 ?가 있다면 (?y)는 \x -> x ? y를 짧게 쓴 것이고, (y?)는 \x -> y ? x를 짧게 쓴 것이다. 연산자 섹션을 사용하면 연산자를 자신의 두 피연산자 중 하나에만 부분적으로 적용(partially apply)하고, 그 결과 인자를 하나만 받는 함수를 얻을 수 있다. 다음 예를 보자.

Prelude> (>100) 102
True
Prelude> (100>) 102
False
Prelude> map (*6) [1..5]
[6,12,18,24,30]

함수 합성

다음과 같은 타입의 함수를 정의할 수 있겠는가?

(b -> c) -> (a -> b) -> (a -> c)

한번 시도해보자. 일단 이 함수는 인자가 2개 있고 두 인자 모두 함수이다. 함수의 이름을 거시기라고 하고, 각 인자에 일단 이름을 붙여보자. 함수 인자는 보통 f,g,h 라는 이름을 많이 사용한다.

거시기 f g = ...

이제 ...에 적당한 식을 넣어서 결과가 a -> c인 함수가 되게 만들어야 한다. 람다 추상화를 사용하면 함수를 만들 수 있음을 알고 있으므로 일단 람다를 하나 넣어보자.

거시기 f g = \x -> ...

x의 타입은 a여야 한다. 이 람다의 본문 ...의 타입은 c여야 한다. 타입을 생각해보자. f는 b -> c 타입이고, g는 a -> b 타입이다. x가 a 타입이므로, g에 x를 적용해 b 타입의 값을 얻고, 그 값을 함수 f에 적용해 c 타입의 값을 얻으면 될 것 같다.

거시기 f g = \x -> f (g x)

(퀴즈: g x에 괄호를 쳐야 하는 이유는?)

좋다. 이렇게 만든 거시기 함수는 대체 무슨 쓸모가 있을까? 쓸모가 있기는 한걸까? 그냥 타입을 가지고 장난질하는 예제에 불과한건 아닐까?

중등 수학을 배운 사람은 다 알겠지만 이 함수 거시기는 실제로는 함수 합성(function composition)이다. 수학에서는 작은 동그라미를 사용하지만 하스켈에서는 마침표를 사용해 (.)라는 연산자로 함수 합성이 정의되어 있다. f . g는 g를 먼저 인자에 적용한 다음, 그 결과에 f를 적용하는 연산이다.

함수 합성을 사용하면 간결하고 우아하게 코드를 작성할 수 있다. 통밀 스타일 코딩에 (.)가 유용하다. 데이터 구조에 대해 고수준의 변환을 연속적으로 적용하고 싶을 때 (.)를 써먹을 수 있기 때문이다.

다음 예제를 보자.

myTest :: [Integer] -> Bool
myTest xs = even (length (greaterThan100 xs))

이를 (.)를 사용해 다시 쓰면 다음과 같다.

myTest' :: [Integer] -> Bool
myTest' = even . length . greaterThan100

myTest'가 실제 어떤일이 벌어지는지를 더 간결하고 명확하게 알려준다. myTest'은 단지 더 작은 함수들을 서로 이어붙인 파이프라인에 지나지 않는다. 또, 이 예제를 보면 함수 합성이 왜 “역방향”으로 일어나야 하는지 알 수 있다. 이유는 바로 함수 적용이 역방향이기 때문이다. 사실 코드를 왼쪽에서 오른쪽 방향으로 읽기 때문에 값도 왼쪽에서 오른쪽으로 흐른다고 생각할 수 있다면 좋을 것이다. 즉, x를 f로 변환하는 경우 (x)f와 같이 쓸 수 있다면 좋을 텐데, 불행히도 1734년 알렉시 클로드 클레르(Alexis Claude Clairaut)와 오일러(Euler)가 f(x)라는 표기법을 채택했기 때문에 그 전통을 버릴 수가 없다.

ghci에서 (.)를 살펴보자.

Prelude> :t (.)
(.) :: (b -> c) -> (a -> b) -> a -> c

어라? 잠깐! 마지막 a -> c에는 왜 괄호가 없는걸까?

커링과 부분 적용

예전에 인자가 여럿 있는 함수의 타입이 이상해 보인다고 이야기한 사실을 기억하는가? 다음 함수를 예로 들어보자.

f :: Int -> Int -> Int
f x y = 2*x + y

이전에 이 타입에는 멋진 이유가 있고 나중에 그에 대해 설명한다고 약속했었다. 이제 드디어 그 비밀을 밝힐 때가 됐다! 실제로 하스켈의 모든 함수는 인자가 오직 하나 뿐이다 뭐라고? 하지만 위의 f 함수는 인자가 2개 아닌가? 그렇지 않다. 실제로 f는 인자를 하나(Int)만 받아서 함수(Int -> Int)를 반환하는 함수다. f가 반환하는 함수는 인자를 하나 받아서 최종 결과를 만들어낸다. 실제로 이 f를 다음과 같이 쓸 수도 있다.

f' :: Int -> (Int -> Int)
f' x y = 2*x + y

구체적으로 설명하자면, 함수 타입의 ->는 왼쪽 결합법칙을 따른다. 즉, W -> X -> Y -> Z는 W -> (X -> (Y -> Z))와 같다. 따라서 어떤 타입의 가장 오른쪽에 있는 화살표를 감싸는 괄호는 생략 가능하다.

반면에 함수 적용은 왼쪽 결합법칙을 따른다. 즉, f 3 2는 (f 3) 2로 해석된다. 이런 결합 법칙은 앞에서 f가 인자를 하나 받아서 함수를 반환한다고 설명한 내용과 맞아 떨어진다. f 3 2에서 우리는 Int -> Int 타입의 함수를 반환하는 f 함수에 3를 먼저 적용한다. 따라서서 f 3이 반환하는 함수는 Int를 받아서 6을 더하는 함수다. 이 함수에 다시 2를 적용해야 하므로 (f 3) 2라고 쓸 수 있다. 함수 적용은 왼쪽 결합 법칙을 따르기 때문에 (f 3) 2를 f 3 2라고 줄여쓸 수 있고, 이렇게 표시하면 “인자가 둘 이상인” 함수를 멋지게 표현할 수 있다.

“인자가 여럿인” 람다 식을 보자.

\x y z -> ...

이 식은 실제로는 다음을 편하게 쓰도록 배려한 것일 뿐이다(이를 편리 문법(syntatic sugar)이라고 한다).

\x -> (\y -> (\z -> ...))

마찬가지로 다음과 같은 함수 정의도,

f x y z = ...

다음에 대한 편리 문법일 뿐이다.

f = \x -> (\y -> (\z -> ...))

이런 특징을 활용하면 앞에서 본 합성 함수(거시기 또는 하스켈 프렐류드 .)에서 \x… 등을 등호의 왼쪽으로 옮겨서 다음과 같이 표현할 수 있다.

거시기 :: (b -> c) -> (a -> b) -> a -> c
거시기 f g = f (g x)

이런 식으로 인자가 하나인 함수를 가지고 인자가 여럿인 함수를 표현하는 방법을 커링(currying)이라고 부른다. 커링이라는 용어는 영국 출신 수학자이자 논리학자인 하스켈 커리(Haskell Curry, 1900~1982)의 이름을 본딴 것이다. 그는 (이 강의가 열린) UPenn에서 에니악(ENIAC) 개발을 돕기도 했다. 실제 커링의 아이디어를 맨 처음 발견한 사람은 모세 이샤이비치 숀핑켈(영어이름: Moses Schönfinkel, 러시아어이름: Моисей Исаевич Шейнфинкель)이었고 커리도 숀핑켈이 맨 처음 생각한 아이디어라고 인정했지만 (이미 커링이라고 부르기 시작하기도 했고, 아무래도 숀핑켈링은 부르기 힘들기도 하고, 러시아 사람이기도 하고 등등의 이유로) 커링이 이런 표현 방식을 가리키는 용어로 정착했다.

함수가 실제 인자를 두개 받아야 한다면 튜플을 사용할 수 있다. 즉, 다음과 같은 함수도 “인자를 2개 받는 함수”로 생각할 수 있다.

f'' :: (Int,Int) -> Int
f'' (x,y) = 2*x + y

하지만 이 함수를 튜플 타입의 인자를 하나만 받는 함수라고 생각할 수도 있다. 이렇게 인자가 2개인 함수를 표현하는 두가지 방식을 오기는 함수로 하스켈 표준 라이브러리에는 curry와 uncurry가 있다. 각각은 숀핑켈의 이름을 빌리면 다음과 같이 정의할 수 있다.

schönfinkel :: ((a,b) -> c) -> a -> b -> c
schönfinkel f x y = f (x,y)

-- 혹시 위 정의를 따라가지 못하는 독자는 다시 한번 다음 정의와 위 정의가 같음을 기억하라
schönfinkel' = \f -> \x -> \y -> f (x,y)

unschönfinkel :: (a -> b -> c) -> (a,b) -> c
unschönfinkel f (x,y) = f x y

-- 역시 위 정의도 다음과 같이 생각할 수 있다
-- tuple@(x,y)는 tuple이라는 인자를 받아서 튜플의 두 값을 x,y로 분해해 사용함을 보여준다 
unschönfinkel'   = \f -> \tuple -> f (fst tuple) (snd tuple)
unschönfinkel''  = \f -> \tuple@(x,y) -> f x y
unschönfinkel''' = \f -> \(x,y) -> f x y

특히 어떤 튜플 값이 있을 때 그 튜플을 함수에 적용해야 한다면 uncurry가 유용하다.

Prelude> uncurry (+) (2,3)
5

부분 적용

하스켈에서는 커링을 사용하기 때문에 부분 적용(partial application)을 활용하기 쉽다. 부분 적용이란 인자가 여럿 있는 함수에서 일부 인자만을 제공하고 나머지 인자는 제공하지 않고 비워두는 것이다. 하지만 하스켈에서는 인자가 여럿 있는 함수가 없다! 그래서 하스켈에서는 함수의 첫번째 인자만을 부분 적용하면 두번째 이후의 나머지 인자를 필요로 하는 새로운 함수를 얻을 수 있다.

하지만 하스켈에서 첫번째 인자가 아닌 중간의 인자를 부분적용하기는 쉽지 않다. 다만 중위 연산자(infix operator)의 경우는 예외다. 앞에서 본 것처럼 ?라는 중위 연산자가 있으면 (?arg)나 (arg?)를 사용해 두 인자중 하나를 부분적용할 수 있다(이를 섹션(section) 이라고 부른다). 부분 적용을 감안해 파라미터 순서를 정할 때 중요한 기법이 있다. 그 기법은 바로 “변화할 여지가 가장 적은 것을 앞에 배치하고 자주 변하는 파라미터를 뒤에 배치”하는 것이다. 즉 인자 중에서 같은 값이 적용되는 경우가 가장 자주 있는 인자를 맨 앞에 배치하고, 가장 자주 바뀌는 인자를 맨 뒤에 배치해야 한다.

통밀 프로그래밍

지금까지 배운 내용을 바탕으로 “통밀 프로그래밍” 스타일의 코딩을 시도해보자. 다음 foobar를 생각해보자.

foobar :: [Integer] -> Integer
foobar []     = 0
foobar (x:xs)
  | x > 3     = (7*x + 2) + foobar xs
  | otherwise = foobar xs

이 코드는 단순하긴 하지만 하스켈 스타일의 코드라고는 할 수 없다. 문제는 다음과 같다.

• 한번에 너무 많은 일을 한다.
• 너무 저수준에서 작업을 수행한다.

리스트의 각 원소에 대해 할 일을 생각하는 대신에, 전체 입력 리스트를 전체적으로 어떻게 변환시켜 나가야 할지를 생각할 수 있다. 이때 우리가 익히 알고 있는 기존 재귀 패턴을 활용해야 한다. 다음은 foobar를 좀 더 하스켈다운 코드로 바꾼 것이다.

foobar' :: [Integer] -> Integer
foobar' = sum . map (\x -> 7*x + 2) . filter (>3)

이 foobar' 정의는 3가지 함수를 파이프라인처럼 연결한다. 먼저 리스트에서 3보다 큰 원소를 filter로 선택한다. 이렇게 골라낸 3을 초과하는 원소들에 대해 람다로 정의한 산술 연산을 적용한다. 그 후 산술 연산을 적용한 결과를 모두 합한다.

이 예에서 map이나 filter가 부분 적용되었음에 유의하라. 예를 들어 filter의 타입은 (a -> Bool) -> [a] -> [a]이고, filter에게 Integer -> Bool 타입의 함수인 (>3)을 적용하면 [Integer] -> [Integer] 함수를 얻을 수 있다. 이 함수는 [Integer]에 적용할 수 있는 다른 함수들과 쉽게 합성할 수 있다.

이런식으로 코딩을 하면 함수를 정의할 때 인자를 특별히 참조하지 않고 코딩하게 된다. 어떤 의미에서 이는 함수가 어떤 일을 하는가(what a function does)보다 그 함수가 어떤 존재인가(what a function is)를 기술하는 것이다. 이를 포인트 프리(point-free) 스타일의 프로그래밍이라고 부른다. 위의 예제를 보면 알 수 있는 것처럼 이런 스타일의 코드는 상당히 아름답다.

포인트 프리 프로그래밍

포인트 프리 프로그래밍은 (.) 연산자(마침표=point)를 사용하지 않는 프로그래밍이 아니다. 여기서 포인트라는 말은 함수가 적용되는 대상인 값을 가리키는 변수를 의미한다. 예를 들어 다음을 보자.

sum (x:xs) = x + sum xs
sum [] = 0

이 코드에서는 x,xs,[] 등의 인자가 직접 드러나 있다. 이런 경우는 포인트 프리 프로그램이 아니다. 하지만 이를 조금 있다 배울 foldr을 사용해 다음과 같이 정의하면 인자가 없기 때문에 포인트 프리 스타일이 된다.

sum = foldr (+) 0

더 나아가 항상 포인트 프리 스타일을 고수하자는 사람도 있다. 예를 들어 IRC #haskell 채널에 있는 lambdabot은 함수를 포인트 프리 식으로 바꿔주는 @pl이라는 명령을 제공한다. 하지만 아래 결과를 보면 알 수 있듯이 항상 포인트프리로 만드는게 코드를 더 개선 하는 것은 아니다.

@pl \f g x y -> f (x ++ g x) (g y)
join . ((flip . ((.) .)) .) . (. ap (++)) . (.)

폴드

리스트에 대한 재귀 패턴 중에 폴드(fold)에 대해 알아보자. 다음 세 함수를 보면 공통 패턴을 찾을 수 있다. 셋 다 리스트에서 원소를 어떤 방법에 의해 하나로 묶는다.

sum' :: [Integer] -> Integer
sum' []     = 0
sum' (x:xs) = x + sum' xs

product' :: [Integer] -> Integer
product' [] = 1
product' (x:xs) = x * product' xs

length' :: [a] -> Int
length' []     = 0
length' (_:xs) = 1 + length' xs

이 세 함수의 공통점과 다른점이 무엇일까? 언제나처럼 고차 함수를 사용하면 공통 부분과 달라지는 부분을 쉽게 추상화할 수 있다.

fold :: b -> (a -> b -> b) -> [a] -> b
fold z f []     = z
fold z f (x:xs) = f x (fold z f xs)

fold의 엑기스만 뽑아보면 결국 리스트에서 []를 z로 대치하고, (:)를 f로 대치한다. 즉, 다음과 같다.

fold f z [a,b,c] == a `f` (b `f` (c `f` z))

(이런 관점에서 fold를 생각해보면 리스트가 아닌 다른 데이터 타입에 대해 fold를 어떻게 더 일반화할 수 있는지 알수도 있을 것이다.)

이제 fold를 써서 앞의 세 함수를 다시 써보자.

sum''     = fold 0 (+)
product'' = fold 1 (*)
length''  = fold 0 (\_ s -> 1 + s)

(여기서 \_ s -> 1 + s는 (\_ -> (1+))나 (const (1+))로도 적을 수 있다)

const (1+)

const는 다음과 같다.

const :: a -> b -> a
const x _ = x

따라서 const (1+)의 타입은 b->(Int->Int)가 되며(실제 타입은 이보다 더 복잡하지만 여기서는 이정도로 정리하자), 하는 일은 첫번째 인자는 무시하고 두번째 인자(Int 타입)를 받아서 1 더해서 반환하는 것이다.

물론 프렐류드에는 fold와 같은 역할을 하는 함수가 이미 들어있다. 다만 이름은 foldr이다. foldr의 인자는 여기서 본 정의와 순서가 다르지만 기능은 동일하다. 다음은 foldr로 정의할 수 있는 몇가지 프렐류드 함수들이다. 각각을 한번 foldr로 정의해 보라(숙제로 남겨둔다).

length :: [a] -> Int
sum :: Num a => [a] -> a
product :: Num a => [a] -> a
and :: [Bool] -> Bool
or :: [Bool] -> Bool
any :: (a -> Bool) -> [a] -> Bool
all :: (a -> Bool) -> [a] -> Bool

또 foldl도 있다. foldl은 “왼쪽부터 폴드”하는 함수다. foldr과 foldl을 풀어쓰면 다음과 같다.

foldr f z [a,b,c] == a `f` (b `f` (c `f` z))
foldl f z [a,b,c] == ((z `f` a) `f` b) `f` c

하지만 일반적으로는 Data.List에 정의된 foldl'을 쓸 것을 권장한다. 이 foldl'은 foldl과 같은 일을 하지만 효율이 더 좋다.

연습문제

연습문제 1 - 통밀 프로그래밍

다음 두 함수를 통밀 프로그래밍 스타일로 재작성하라. 두 함수를 각각 데이터구조 전체를 점진적으로 변환하는 파이프라인을 사용해 재구현하라. 다시 구현한 각 함수의 이름을 fun1'과 fun2'으로 붙여라.

fun1 :: [Integer] -> Integer
fun1 [] = 1
fun1 (x:xs)
  | even x    = (x - 2) * fun1 xs
  | otherwise = fun1 xs

fun2 :: Integer -> Integer
fun2 1 = 0
fun2 n | even n    = n + fun2 (n ‘div‘ 2)
       | otherwise = fun2 (3 * n + 1)

힌트: iterate(문서)와 takeWhile(문서)을 사용하고 싶을 것이다. 프렐류드 문서에서 그 두 함수가 어떤 일을 하는지 살펴보라.

연습문제 2 - 트리에 대한 폴드

이진 트리 데이터 구조의 정의를 한번 다시 떠올려보자. 이진 트리의 높이(height)는 루트(root)로부터 잎(리프,leaf)에 이르는 경로(path) 중 가장 긴 경로의 길이다. 예를 들어 노드가 1개뿐인 트리의 높이는 0이고 루트와 루트의 두 자식으로 이뤄진 트리의 높이는 1이다. 어떤 이진 트리 루트의 오른쪽 하위 트리와 왼쪽 하위 트리의 높이 차이가 1이 또는 0이고, 각각의 하위 트리도 균형 트리인 경우, 그 이진 트리를 균형 트리(balanced tree)라고 한다.

다음 데이터 구조를 사용해 이진 트리를 표현하라. Node에 있는 Integer는 해당 노드의 높이를 표현한다.

data Tree a = Leaf
            | Node Integer (Tree a) a (Tree a)
  deriving (Show, Eq)

이제 주어진 리스트로부터 균형 이진 트리를 만들어내는 다음과 같은 함수를 작성하라. 이때 foldTree는 리스트에 대해 foldr을 사용해 트리를 만들어야 한다.

foldTree :: [a] -> Tree a
foldTree = ...

예를 들어, “ABCDEFGHIJ”로 만들 수 있는 균형 2진 트리 중 하나는 다음과 같다.

foldTree "ABCDEFGHIJ" ==
  Node 3
    (Node 2
      (Node 0 Leaf ’F’ Leaf)
      ’I’
      (Node 1 (Node 0 Leaf ’B’ Leaf) ’C’ Leaf))
    ’J’
    (Node 2
      (Node 1 (Node 0 Leaf ’A’ Leaf) ’G’ Leaf)
      ’H’
      (Node 1 (Node 0 Leaf ’D’ Leaf) ’E’ Leaf))

이를 그림으로 표현하면 다음과 같다. 여러분의 해는 이와 다르게 노드를 배치할 수도 있다. 하지만 출력은 반드시 균형 2진 트리여야 한다. 또한 각 하위 트리의 높이로 제대로 계산된 값이 들어가 있어야 한다.

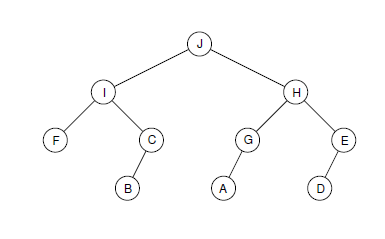
연습문제 2++ : 균형 트리 확인하기

연습문제 2에서 만든 트리가 균형트리인지 확인하는 함수를 작성하라.

isBalanced :: Tree a -> Bool

연습문제 3: 폴드 연습!

연습문제 3.1

다음 함수를 구현하라. 입력 리스트에 True가 홀수개 들어 있으면 True를, 그렇지 않으면 False를 반환한다.

xor :: [Bool] -> Bool

예를 들면 다음과 같다.

xor [False, True, False] == True
xor [False, True, False, False, True] == False

foldr이나 foldl을 사용해 xor를 구현해야 한다.

연습문제 3.2

map을 폴드를 사용해 구현하라. 즉, 다음 정의를 완성하되 map'이 map과 같은 일을 하게 만들라.

map’ :: (a -> b) -> [a] -> [b]
map’ f = foldr ...

연습문제 3.3

foldl을 foldr로 구현하라.

myFoldl :: (a -> b -> a) -> a -> [b] -> a
myFoldl f base xs = foldr ...

(힌트: foldl과 foldr의 적용이 어떻게 정의되는지 자세히 살펴보라.)

foldr f z [x1, x2, ..., xn] == x1 ‘f‘ (x2 ‘f‘ ... (xn ‘f‘ z)...)
foldl f z [x1, x2, ..., xn] == (...((z ‘f‘ x1) ‘f‘ x2) ‘f‘...) ‘f‘ xn

연습문제 4 - 소수 찾기

순다람의 체를 읽어보고, 그 알고리즘을 함수 합성을 사용해 구현하라. 여러분이 만든 함수는 주어진 정수 n에 대해 2n + 2까지 이르는 모든 홀수인 소수를 생성해야 한다.

sieveSundaram :: Integer -> [Integer]
sieveSundaram = ...

도움이 될 내용을 한가지 정리한다. 두 리스트의 데카르트 곱(Cartesian Product)을 구하는 함수 cartProd를 정의할 수 있다. cartPorod는 각 리스트에서 하나씩 원소를 뽑아서 만들 수 있는 모든 순서쌍(튜플)을 반환한다.

cartProd [1,2] [’a’,’b’] == [(1,’a’),(1,’b’),(2,’a’),(2,’b’)]

이를 리스트 컴프리핸션(comprehension)으로 다음과 같이 쓸 있다. 아직 다루지 않은 내용이므로 궁금한 사람은 구글이나 하스켈 책을 찾아보라.

cartProd :: [a] -> [b] -> [(a, b)]
cartProd xs ys = [(x,y) | x <- xs, y <- ys]